Le mouvement de Mars étudié par les Anciens Grecs

Pour les Anciens de l’Antiquité, Mars est une planète remarquable. Ils lui ont ainsi donné de nombreux noms. Ils ont été également frappés par son mouvement irrégulier, un vrai casse-tête pour les astronomes à travers les siècles. Découvrons, dans un premier temps, les solutions proposées par les Anciens Grecs pour résoudre le mystère du mouvement de Mars.

Énigme : pourquoi Mars swingue dans le ciel ?

Comme les quatre autres planètes visibles à l’œil nu (Mercure, Vénus, Jupiter et Saturne), Mars se déplace d’est en ouest par rapport aux étoiles. Cependant, à certaines périodes, elle se déplace différemment. Cela se passe juste avant que Mars soit à l’opposé du Soleil dans le ciel, une configuration que l’on appelle opposition. À ce moment, Mars stoppe son mouvement est-ouest, part dans le sens inverse avant de s’arrêter à nouveau et de repartir dans son sens habituel.

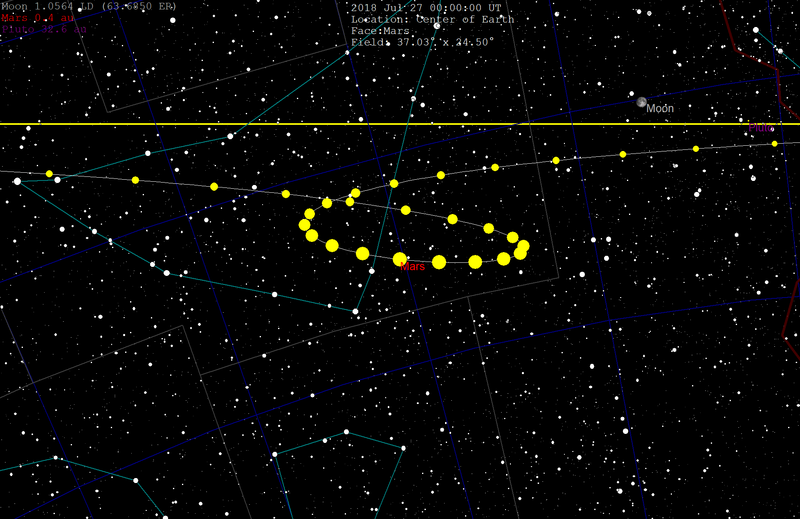
Mars' retrograde motion in 2018 near opposition

Illustration du mouvement rétrograde de Mars aux alentours de son opposition en 2018. Crédit: Tomruen (CC-BY-SA 4.0 via Wikimedia Commons)

Les Anciens Grecs sont les premiers à chercher des explications rationnelles du mouvement rétrograde de Mars. Pour eux, la Terre est au centre dans l’univers et le monde céleste est parfait. Donc, les orbites des étoiles et des planètes doivent être des cercles parfaits. Cependant, les mouvements observés des planètes ne correspondent pas à cette perfection circulaire. Cette non-correspondance est évidente pour nous, qui savons que la Terre et les autres planètes tournent autour du Soleil et que leur orbites ne sont pas tout à fait circulaires. Or, ce savoir n’existait pas dans l’Antiquité. Par conséquent, pour « conserver la perfection » des mouvements planétaires, les Anciens ont dû user de leur imagination et ingéniosité pour trouver un modèle correspondant.

Eudoxe de Cnide et la théorie des sphères homocentriques

Un premier modèle a été proposé par Eudoxe de Cnide, un mathématicien contemporain de Platon (4e siècle av. J.-C.). Pour Eudoxe, le mouvement de chaque astre est une combinaison de mouvements circulaires commandés par un groupe de sphères qui lui sont propres : les sphères homocentriques. Chacune de ces sphères ont la Terre pour centre, mais tournent autour d’axes de rotation différents à des vitesses différentes. De plus, les sphères les plus à l’extérieur entraînent dans leur rotation les sphères qui sont à l’intérieur d’elles. Chaque planète a quatre sphères. La Lune et le Soleil ont chacun trois sphères et la voûte céleste a une sphère.

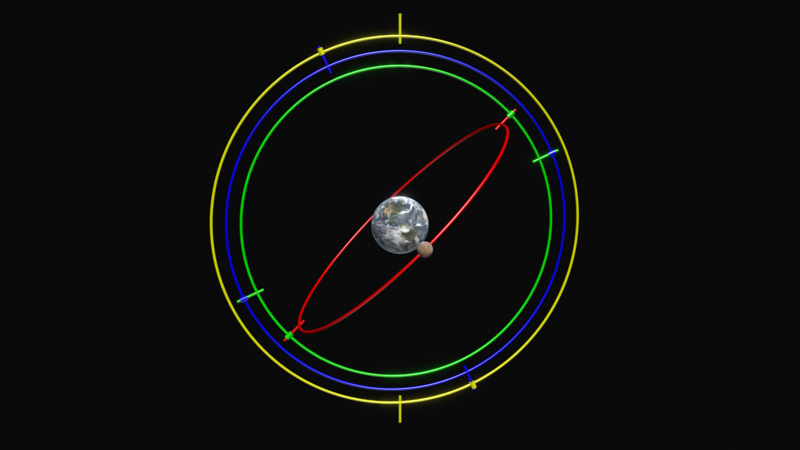
Le modèle du mouvement planétaire d’Eudoxe de Cnide. Chacune de ses sphères homocentriques est représentée ici comme un anneau qui tourne sur l’axe représenté. Crédit: Thehopads (CC-BY-4.0 via Wikimedia Commons)

Les quatre sphères homocentriques associées à une planète correspondent à ceci :

La sphère la plus à l’extérieur explique le mouvement journalier de la planète autour de la Terre
La seconde sphère explique le mouvement de la planète le long du zodiaque, une bande de la voûte céleste dont l’orbite du Soleil est au milieu
La troisième et la quatrième sphères expliquent le mouvement rétrograde de la planète.

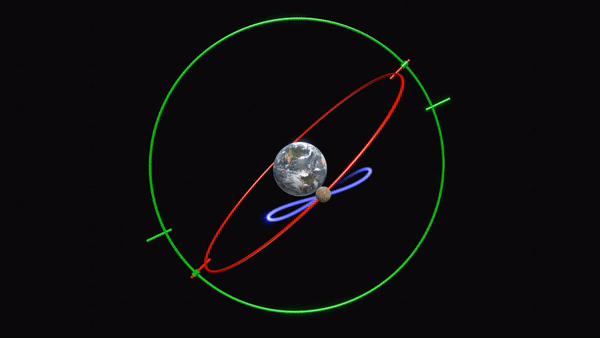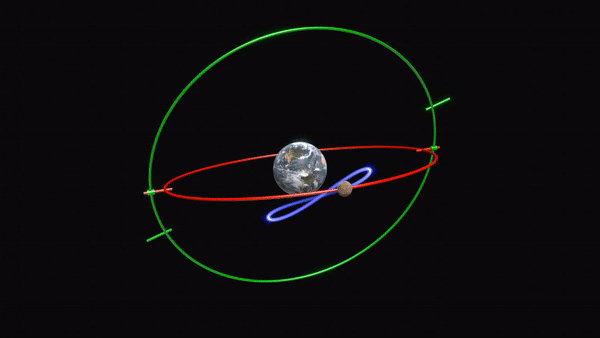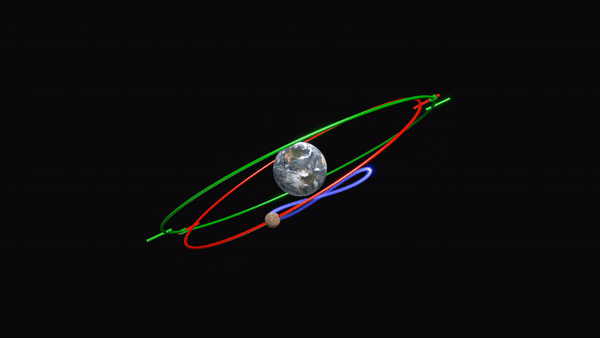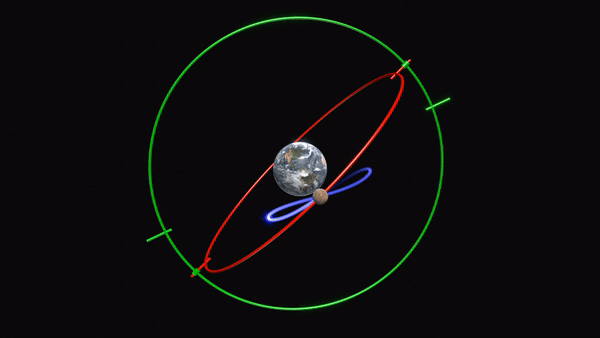
Animation représentant le modèle de mouvement planétaire rétrograde d’Eudoxe de Cnide. Les deux sphères homocentriques les plus profondes de son modèle sont représentées ici sous forme d’anneaux. Chacune tournent avec la même période mais dans des directions opposées, déplaçant la planète le long d’une figure en forme de huit. Crédit: Thehopads (CC-BY-4.0 via Wikimedia Commons)

Pour plus d’informations sur le modèle des sphères homocentriques, vous pouvez consulter la page web (en anglais) de The History of Physics.

Le modèle des sphères homocentriques permet de reproduire de façon qualitative le mouvement rétrograde de planètes comme Mars. Mais elle n’est pas suffisante pour expliquer certains phénomènes. Ainsi, il ne peut pas expliquer pourquoi la luminosité des planètes change au cours du temps. Pour Mars, cette luminosité peut varier d’un facteur cinquante.

Aristarche de Samos et le premier modèle héliocentrique

Vers -250 av. J.-C., Aristarche de Samos propose le premier modèle héliocentrique de l’Histoire. « Héliocentrique » se réfère à un univers avec le Soleil au centre alors que la Terre et les autres planètes tournent autour de lui. Voilà un modèle bien plus proche de la réalité que celui d’Eudoxe de Cnide ! Avec un tel modèle, Aristarche a résolu d’un coup le problème du mouvement rétrograde de Mars et sa variation de luminosité au cours du temps.

En effet, l’orbite de Mars est à l’extérieur de celle de la Terre et Mars tourne plus lentement autour du Soleil que cette dernière. Quand Mars s’approche de son point orbital le plus proche de la Terre, alors, comme la Terre tourne plus vite autour du Soleil, cela crée un effet de projection qui donne pendant un moment l’impression que la planète tourne dans l’autre sens. Le schéma ci-dessous illustre ce phénomène. Vous pouvez aussi essayer de faire cette expérience vous-même. Faites bouger lentement votre doigt de droite à gauche, puis tourner votre tête dans le même sens, mais plus rapidement que votre doigt. Par un effet de projection, vous aurez alors l’impression que votre doigt bouge dans l’autre sens.

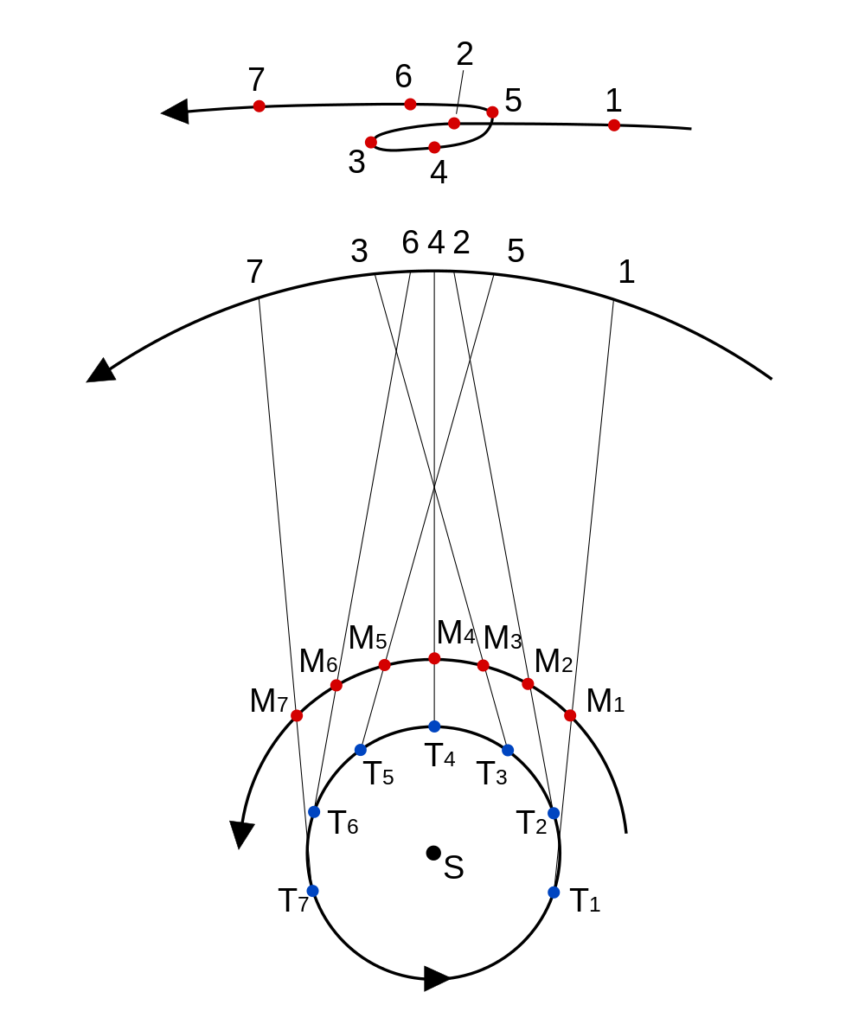
Reconstruction du mouvement rétrograde apparent de Mars vu de la Terre. Crédit : MLWatts via Wikimedia Commons.

Malheureusement, Aristarche a été trop en avance sur son temps. En effet, son modèle ne reproduit pas tout à fait les mouvements observés, car l’astronome a supposé entre autres que les orbites des planètes sont circulaires. Or, ce n’est pas tout à fait le cas, comme nous le verrons dans le prochain billet. À cause de cela, et aussi parce que l’idée d’une Terre en mouvement n’était pas concevable à l’époque, les savants grecs postérieurs sont retournés au système géocentrique.

Des orbites dans des épicycles

Avec la Terre au centre de l’univers, il a fallu trouver une astuce pour expliquer les mouvements rétrogrades des planètes. Quelques savants, dont Appolonios et Hipparque (2e siècle av. J.-C.), ont alors introduit les épicycles. Un épicycle est un cercle dont le centre décrit un cercle (déférent) dans son mouvement. Dans un modèle géocentrique, le centre du déférent est le centre de la Terre (ou en est très proche), et la planète se meut au bord de l’épicycle qui « roule » le long du déférent. En retraçant le mouvement de la planète, on obtient une courbe pas très différente d’un dessin fait avec un Spirographe, comme on le voit dans le schéma ci-dessous.

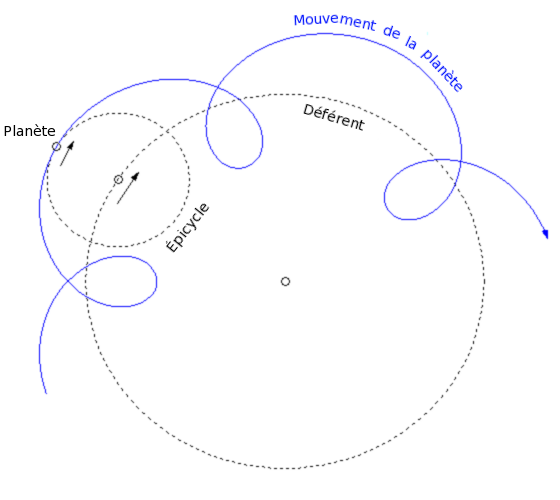
Schéma d'un épicycle d'une planète et de son déférent.

Dans le modèle de Ptolémée, les planètes tournent sur un épicycle qui lui-même tourne sur un déférent. Crédit : Dhenry (CC-BY 4.0 via Wikimedia Commons)

L’introduction des épicycles a été une véritable révolution en astronomie. Elle explique la rétrogradation des planètes quand elles s’approchent de la Terre. De plus, contrairement au modèle d’Eudoxe de Cnide, il tiennent aussi en compte des variations de luminosité des planètes. Pour mieux correspondre aux mouvements observés, on peut notamment faire varier les vitesses des épicycles ou centrer le déférent un tout petit peu en dehors du centre de la Terre.

Le modèle de Ptolémée

C’est avec Claude Ptolémée (2e siècle apr. J.-C.) que le système des épicycles a atteint son plus haut point de sophistication. Parmi ses améliorations, décrites dans son livre l’Almageste (« le Plus Grand »), Ptolémée a introduit le concept du point équant. En effet, il a déduit que la vitesse angulaire des astres n’est pas uniforme par rapport au centre du déférent mais par rapport à un point distinct. Ce point est le point équant. Il se situe sur la ligne qui relie le centre de la Terre et le centre du déférent (distinct du centre de la Terre) et est symétrique au centre de la Terre par rapport au centre du déférent.

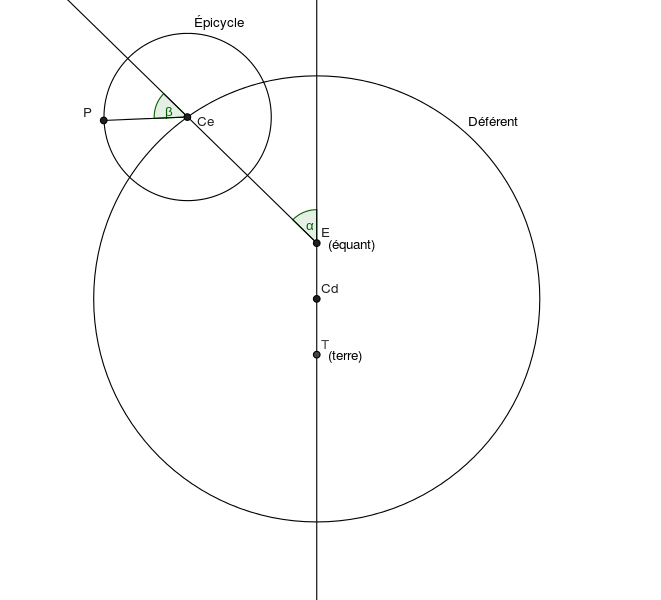
Trajectoire d’une planète dans le modèle de Ptolémée avec utilisation d’un déférent excentré, d’un épicycle et du point équant. Crédit : HB (CC-BY-SA 3.0 via Wikimedia Commons)

Le modèle de Ptolémée est fort complexe et artificiel. Mais, pendant plus de 1300 ans, il est resté le modèle de référence des astronomes d’Occident, de l’Empire byzantin et du Monde arabe. Le système a beau être faux, il marche. De plus, avec la précision des observations astronomiques de l’époque, on n’a pas pu révéler les contradictions de ce modèle. Il a fallu attendre le début de la Renaissance pour que l’on commence à ébranler le consensus du géocentrisme. Mais ça, nous le verrons dans le prochain billet.

Référence

William Sheehan, The Planet Mars: A History of Observation and Discovery. – Chapter 1 Motions of Mars, The University of Arizona Press, The Arizona Board of Regents, 1996.